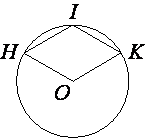Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
HO=KO (т.к. это радиусы окружности)
HO=KO=HI=IK (по
определению ромба)
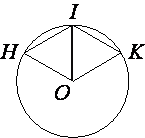Проведем отрезок OI.
OI тоже радиус окружности, следовательно HO=KO=HI=IK=OI
Следовательно, треугольники HIO и KIO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /OKI=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Стороны AC, AB, BC треугольника ABC равны 3√
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: