
 Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
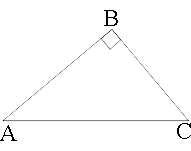 Введем обозначения как показано на рисунке.
Введем обозначения как показано на рисунке.
AB и BC - катеты, AC -
гипотенуза.
По
теореме Пифагора:
AC2=AB2+BC2
AC2=122+162
AC2=144+256
AC2=400
AC=√400=20
Ответ: 20
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
 В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
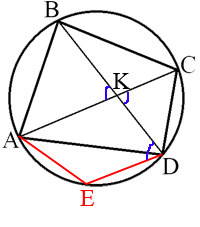 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
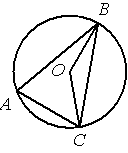 Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
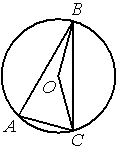 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Комментарии: