
 Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Вариант №1 (Предложил пользователь Людмила)
По второму свойству вписанной в четырехугольник окружности:
AB+CD=BC+AD
7+14=10+AD
AD=7+14-10=11
Ответ: 11
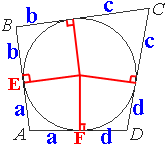 AB и AD - это
касательные к окружности.
AB и AD - это
касательные к окружности.Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
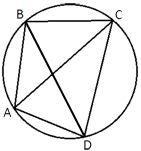 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 2450√
Площадь прямоугольного треугольника равна 2450√
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=28.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=28.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Комментарии:
(2017-05-14 20:24:54) Администратор: Людмила, спасибо большое за Ваше решение. Опубликовано от Вашего имени.
(2017-05-13 18:58:46) Людмила: Можно использовать теорему о том, что окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны. AB+CD=BC+AD, 7+14=10+AD