Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Рассмотрим каждое утверждение:
1) "Любой квадрат является ромбом", это утверждение верно, т.к.
квадрат удовлетворяет определению
ромба.
2) "Против равных сторон треугольника лежат равные углы", это утверждение верно (по свойству
равнобедренного и
равностороннего треугольников).
3) "Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности", это утверждение верно. Эта система (точка и окружность) имеет
ось симметрии - прямая проведенная через данную точку и центр окружности. Соответственно, если можно провести одну
касательную, то можно провести и вторую, симметричную первой.
Ответ: 1), 2) и 3)
Поделитесь решением
Присоединяйтесь к нам...
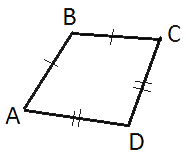В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
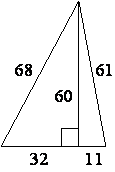Найдите площадь треугольника, изображённого на рисунке.
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: