
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Рассмотрим каждое утверждение:
1) "Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника". Центр
вписанной окружности любого треугольника - точка пересечения
биссектрис (по
свойству вписанной окружности). А в
равнобедренном треугольнике высота, проведенная к основанию является и
биссектрисой и медианой (
свойство). Следовательно, это утверждение верно.
2) "Ромб не является параллелограммом", это утверждение неверно, т.к. противоречит
определению ромба.
3) "Сумма острых углов прямоугольного треугольника равна 90°". В теореме о сумме углов треугольника говорится, что сумма всех углов треугольника равна 180°. В прямоугольном треугольнике один из углов равен 90°, следовательно, сумма двух оставшихся углов равна 180°-90°=90°. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
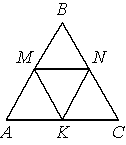 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Синус острого угла A треугольника ABC равен 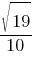 . Найдите CosA.
. Найдите CosA.
Комментарии: