
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ603 –Є–Ј 1087 |
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –љ–∞ –µ–≥–Њ –Љ–µ–і–Є–∞–љ–µ BM –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ K —В–∞–Ї, —З—В–Њ BK:KM=4:1.–Я—А—П–Љ–∞—П AK –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ P.–Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –љ–∞ –µ–≥–Њ –Љ–µ–і–Є–∞–љ–µ BM –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ K —В–∞–Ї, —З—В–Њ BK:KM=4:1.–Я—А—П–Љ–∞—П AK –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ P.–Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
BM -
–Љ–µ–і–Є–∞–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–°,
—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Њ–љ–∞ –і–µ–ї–Є—В —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ –і–≤–∞ —А–∞–≤–љ—Л—Е –њ–Њ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ (
—Б–≤–Њ–є—Б—В–≤–Њ –Љ–µ–і–Є–∞–љ—Л).
SABM=SCMB=SABC/2
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABM –Є –њ—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г –Є–Ј –≤–µ—А—И–Є–љ—Л –Р.
 –Т—Л—Б–Њ—В–∞ h —В–∞–Ї –ґ–µ —П–≤–ї—П–µ—В—Б—П
–≤—Л—Б–Њ—В–Њ–є –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ ABK –Є AKM.
–Т—Л—Б–Њ—В–∞ h —В–∞–Ї –ґ–µ —П–≤–ї—П–µ—В—Б—П
–≤—Л—Б–Њ—В–Њ–є –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ ABK –Є AKM.
–Ч–љ–∞—З–Є—В –Є—Е –њ–ї–Њ—Й–∞–і–Є:
SABK=h*BK*1/2
SAKM=h*KM*1/2
–Э–∞–є–і–µ–Љ –Њ—В–љ–Њ—И–µ–љ–Є–µ —Н—В–Є—Е –њ–ї–Њ—Й–∞–і–µ–є:
SABK/SAKM=(h*BK*1/2)/(h*KM*1/2)
SABK/SAKM=BK/KM=4
–Ґ.–µ.
SAKM=SABK/4
SABK+SAKM=SABM=SABC/2
SABK+SABK/4=SABC/2
SABK*5/4=SABC/2
SABK=(SABC/2)*4/5
SABK=2*SABC/5
SAKM=SABK/4=(2*SABC/5)/4=SABC/10
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї CK –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AKM –Є CKM.
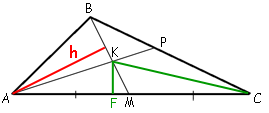 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г KF. –≠—В–∞
–≤—Л—Б–Њ—В–∞ —П–≤–ї—П–µ—В—Б—П –Њ–±—Й–µ–є –і–ї—П –Њ–±–Њ–Є—Е —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Я–ї–Њ—Й–∞–і–Є —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤:
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г KF. –≠—В–∞
–≤—Л—Б–Њ—В–∞ —П–≤–ї—П–µ—В—Б—П –Њ–±—Й–µ–є –і–ї—П –Њ–±–Њ–Є—Е —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Я–ї–Њ—Й–∞–і–Є —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤:
SAKM=KF*AM*1/2
SCKM=KF*CM*1/2
KF=CM (—В–∞–Ї –Ї–∞–Ї BM-
–Љ–µ–і–Є–∞–љ–∞), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ SAKM=SCKM=SABC/10
–Ґ–Њ–≥–і–∞ SCKB=SCMB-SCKM=SABC/2-SABC/10=5*SABC/10-SABC/10=4*SABC/10=2*SABC/5
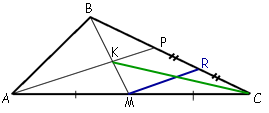 –Т–µ—А–љ–µ–Љ—Б—П –Ї –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–Љ—Г —А–Є—Б—Г–љ–Ї—Г –Є –њ—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї MR, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–є AP.
–Т–µ—А–љ–µ–Љ—Б—П –Ї –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–Љ—Г —А–Є—Б—Г–љ–Ї—Г –Є –њ—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї MR, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–є AP.
–Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ APC MR -
—Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П, —В–∞–Ї –Ї–∞–Ї –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г AC –Є –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞ AP.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є, PR=RC.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є MBR –Є KBP.
∠MBR - –Њ–±—Й–Є–є –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤.
∠BKP=∠BMR, —В–∞–Ї –Ї–∞–Ї –Њ–љ–Є
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ—Л–µ (–і–ї—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е KP –Є MR –Є —Б–µ–Ї—Г—Й–µ–є MB).
–Ч–љ–∞—З–Є—В, –њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г, –і–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є
–њ–Њ–і–Њ–±–љ—Л.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
BM/BK=BR/BP
(BK+KM)/BK=(BP+PR)/BP
1+KM/BK=1+PR/BP
KM/BK=PR/BP=1/4 (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є)
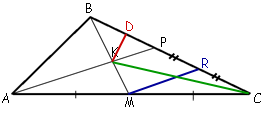 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г KD, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г KD, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
KD - —П–≤–ї—П–µ—В—Б—П
–≤—Л—Б–Њ—В–Њ–є –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ KBP –Є KCP.
SKBP=KD*BP*1/2
SKCP=KD*CP*1/2=KD*(PR+CR)*1/2=KD*(2PR)*1/2
–Э–∞–є–і–µ–Љ –Њ—В–љ–Њ—И–µ–љ–Є–µ —Н—В–Є—Е –њ–ї–Њ—Й–∞–і–µ–є:
SKBP/SKCP=(KD*BP*1/2)/(KD*(2PR)*1/2)
SKBP/SKCP=BP/(2PR)=(BP/PR)/2=(4/1)/2=2
SKBP=2*SKCP
SCKB=2*SABC/5=SKBP+SKCP=2*SKCP+SKCP=3*SKCP
2*SABC/5=3*SKCP
SKCP=2*SABC/15
SKPCM = SCKM+SKCP =
SABC/10+SABC*2/15 = SABC*3/30+SABC*4/30 = SABC*7/30
SABK/SKPCM=(SABC*2/5)/(SABC*7/30)
SABK/SKPCM=(2/5)/(7/30)=(2/5)*(30/7)=(2*30)/(5*7)=(2*6)/7=12/7
–Ю—В–≤–µ—В: 12/7
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
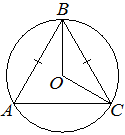 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=57¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –≤ –Ї–Њ—В–Њ—А–Њ–Љ AB=BC –Є ∠ABC=57¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BOC. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ—А–Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–µ AB —В—А–∞–њ–µ—Ж–Є–Є ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ F. –Э–∞–є–і–Є—В–µ AB, –µ—Б–ї–Є AF=8, BF=15.
–С–Є—Б—Б–µ–Ї—В—А–Є—Б—Л —Г–≥–ї–Њ–≤ A –Є B –њ—А–Є –±–Њ–Ї–Њ–≤–Њ–є —Б—В–Њ—А–Њ–љ–µ AB —В—А–∞–њ–µ—Ж–Є–Є ABCD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ F. –Э–∞–є–і–Є—В–µ AB, –µ—Б–ї–Є AF=8, BF=15.
 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Я—А—П–Љ—Л–µ AB –Є CD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, BK=7, DK=14, BC=10. –Э–∞–є–і–Є—В–µ AD.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Я—А—П–Љ—Л–µ AB –Є CD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, BK=7, DK=14, BC=10. –Э–∞–є–і–Є—В–µ AD.
 –Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 45¬∞ –Є 150¬∞, –∞ CD=26.
–Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 45¬∞ –Є 150¬∞, –∞ CD=26.
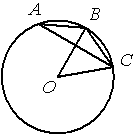 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=50¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=50¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-02-09 15:58:35) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь–∞—И–∞, —А–∞–і—Л, —З—В–Њ –љ–∞—И —Б–∞–є—В –њ–Њ–ї–µ–Ј–µ–љ!
(2015-02-09 15:09:31) –Љ–∞—И–∞: –°–њ–∞—Б–Є–±–Њ, —Б –≤–∞–Љ–Є –ї–µ–≥—З–µ —Г—З–Є—В—М—Б—П!!!