
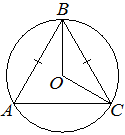 Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
Так как треугольник ABC
равнобедренный, то:
∠BAC=∠BCA=x (по
свойству равнобедренного треугольника)
По
теореме о сумме углов треугольника:
180°=∠BAC+∠BCA+∠ABC
180°=x+x+57°
180°-57°=2x
123°=2x
x=123°/2=61,5°=∠BAC
∠BAC -
вписанный в окружность угол, следовательно градусная мера дуги, на которую он опирается (дуга BC) вдвое больше самого угла:
2*61,5°=123°
∠BOC -
центральный угол, следовательно, он равен градусной мере дуги, на которую он опирается, т.е. 123°
Ответ: 123
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
 В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
Косинус острого угла A треугольника ABC равен 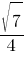 . Найдите sinA.
. Найдите sinA.
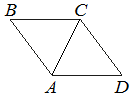 В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Комментарии: