
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
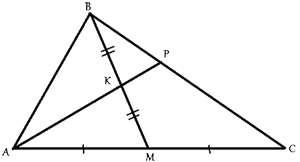 По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
По условию задачи ВМ -
медиана треугольника АВС, следовательно, по
свойству медианы,
площади треугольников АВМ и ВСМ равны, и равны половине площади треугольника АВС.
SABM=SBCM=(SABC)/2.
В свою очередь, AK является медианой для треугольника АВМ, следовательно, по тому же
свойству медианы
SABК=SAKM=(SABM)/2=(SABC)/4.
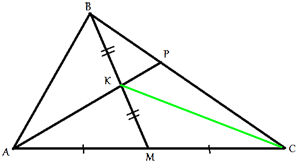 Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
Проведем отрезок СК.
СК является
медианой для треугольника СМВ, следовательно,
SCMK=SCKB=(SCMB)/2=(SABC)/4.
Проведем отрезок МЕ, параллельно АР.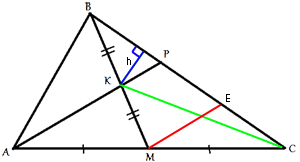 МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
МЕ является
средней линией для треугольника АРС, следовательно (по
теореме о средней линии) СЕ=ЕР. А для треугольника МВЕ
КР является
средней линией, следовательно ВР=ЕР(=СЕ). Т.е. сторона ВС делится на три равные части точками
Р и Е.
Проведем
высоту h, как показано на рисунке. h является общей высотой для треугольников СКВ и СКР.
Выше мы определили, что SCKB=(SABC)/4. Площадь этого же треугольника =(1/2)*h*BC.
SCKP=(1/2)*h*РС=(1/2)*h*(2/3)*ВС=(2/3)*(1/2)*h*BC=(2/3)SCKB=(2/12)SABC
=(1/6)SABC.
SKPCM=SCMK+SCKP=(SABC)/4+(1/6)SABC=(5/12)SABC.
Следовательно отношение SKPMC к SAMK равно ((5/12)SABC)/(1/4)SABC=5/3.
Ответ: SKPMC/SAMK=5/3.
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
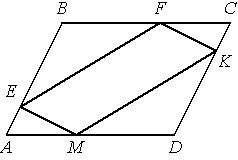 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
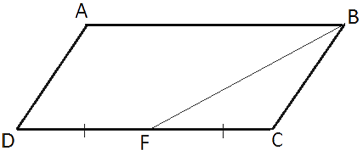 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Комментарии:
(2015-05-24 11:47:05) Администратор: Олеся, высота не обязательно проходит через сам треугольник, она может лежать и вне треугольника, главное, чтобы она была перпендикулярна стороне.
(2015-05-24 07:29:55) Олеся: Я не понимаю,как h может быть высотой для СКР?
(2015-01-23 23:18:12) Администратор: Всеволод, обязательно изучу Ваш вариант и, если он окажется проще, то обязательно добавлю на сайт.
(2015-01-23 13:29:20) Всеволод: Предлагаю вариант без проведения ME. Может кому-то будет проще. Пусть x=S(ABK)=S(AKM)=S(KMC)=S(KBC) Пусть y=S(KBP), тогда S(KPC)=S(KBC)-S(KBP)=x-y Отношение их площадей S(KBP)/S(KPC)=y/(x-y) Отношение площадей S(ABP)/S(APC) будет таким же, как и S(KBP)/S(KPC), ведь у них те же основания BP и PC, только общая вершина уже в А, а не в точке K. S(ABP)/S(APС)=S(KBP)/S(KPC) Набираем площади ABP и APС в наших переменных: S(ABP)/S(APС)=(x+y)/(x+x+(x-y)) Равенство отношений площадей: (x+y)/(3x-y)=y/(x-y), откуда находим x=3y Искомое отношение площадей в наших переменных: S(KPCM)/S(AMK)=((x-y)+x)/x=((3y-y)+3y)/3y=5/3
(2014-09-24 00:20:05) : спасибо
(2014-09-24 00:20:05) : спасибо