
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и угловыми коэффициентами прямых.
ГРАФИКИ
A)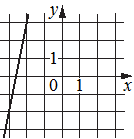 Б)
Б)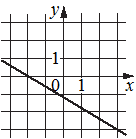 В)
В)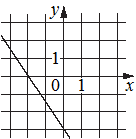 Г)
Г)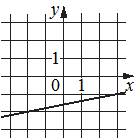
УГЛОВЫЕ КОЭФФИЦИЕНТЫ
1) 0,2
2) 5
3) -1,5
4) -0,6
В таблице под каждой буквой укажите соответствующий номер.
Угловой коэффициент - это коэффициент k.
В данной задаче можно пойти двумя путями: аналитическим и математическим. Пройдемся обоими путями.
Аналитический метод (более быстрый, но менее точный).
Если прямая возрастает слева направо, то коэффициент будет положительным. И чем "круче" возрастает, тем больше коэффициент.
Тогда по графикам видно, что:
Графику А), как самой "круто-возрастающей" прямой, соответствует коэффициент 2) 5, как самый большой.
Графику Г), тоже возрастающему, соответствует коэффициент 1) 0,2, как наименьший из положительных.
Для убывающих прямой коэффициент отрицательный, но чем "круче" убывает, тем меньше коэффициент.
Графику В), как самой "круто-убывающей" прямой, соответствует коэффициент 3) -1,5, как наименьший.
Графику Б), тоже убывающему, соответствует коэффициент 4) -0,6, как наибольший из отрицательных.
| График | А) | Б) | В) | Г) |
| Производная | 2) | 4) | 3) | 1) |
| График | А) | Б) | В) | Г) |
| Производная | 2) | 4) | 3) | 1) |
Поделитесь решением
Присоединяйтесь к нам...
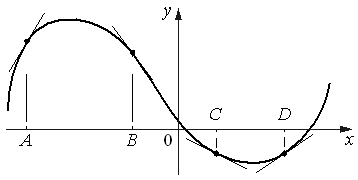 На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| A |
1) 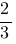
|
| B |
2) 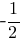
|
| C |
3) 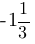
|
| D |
4) 
|
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
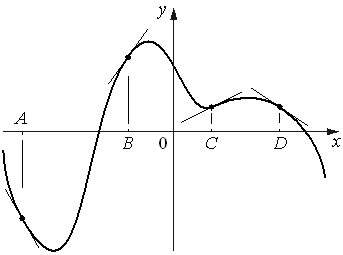
В правом столбце указаны значения производной функции в точках A, B, C
и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
| А | 1) -0,7 |
| B | 2) 1,4 |
| C | 3) -1,8 |
| D | 4) 0,5 |
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч,
на горизонтальной — время в минутах, прошедшее с начала движения автобуса.
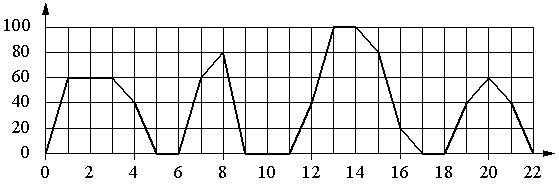
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) 0–4 мин. | 1) была остановка длительностью ровно 1 минута |
| Б) 4–8 мин. | 2) скорость автобуса достигла максимума за всё время движения |
| В) 8–12 мин. | 3) две минуты автобус двигался с постоянной ненулевой скоростью |
| Г) 12–16 мин. | 4) была остановка длительностью 2 минуты |
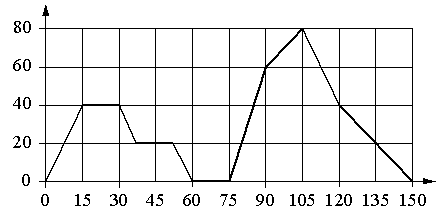 На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
На рисунке точками показаны объёмы месячных продаж холодильников
в магазине бытовой техники. По горизонтали указываются месяцы,
по вертикали — количество проданных холодильников. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников.
| ИНТЕРВАЛЫ ВРЕМЕНИ | ХАРАКТЕРИСТИКИ |
| А) январь-март | 1) продажи за первый и второй месяцы квартала совпадают |
| Б) апрель-июнь | 2) ежемесячный объём продаж достигает максимума за весь период |
| В) июль-сентябрь | 3) за этот период ежемесячный объём продаж увеличился на 300 холодильников |
| Г) октябрь-декабрь | 4) за последний месяц периода было продано меньше 200 холодильников |
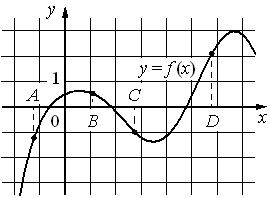 На рисунке изображён график функции y=f(x) и отмечены точки A, B, C и D на оси Ox. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
На рисунке изображён график функции y=f(x) и отмечены точки A, B, C и D на оси Ox. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
| ТОЧКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ И ПРОИЗВОДНОЙ |
| A | 1) значение функции в точке положительно, а значение производной функции в точке отрицательно |
| B | 2) значение функции в точке отрицательно, и значение производной функции в точке отрицательно |
| C | 3) значение функции в точке положительно, и значение производной функции в точке положительно |
| D | 4) значение функции в точке отрицательно, а значение производной функции в точке положительно |
Комментарии: