
При каких значениях m вершины парабол у=–х2+4mх–m и у=х2+2mх–2 расположены по одну сторону от оси х?
Вариант №1 (предложил пользователь Татьяна)
То, что вершины обеих парабол располагаюся по одну сторону от оси Х, означает, что координата "y" обоих вершин или положительна (когда обе вершины находятся выше оси Х), или отрицательна (когда обе вершины находятся ниже оси Х).
Координату "х" можно найти по формуле:
x0=-b/(2a)
Координату "y" можно найти, подставив x0 в функцию.
Тогда для первой функции у=–х2+4mх–m:
x01=-b/(2a)=-4m/(2(-1))=-4m/(-2)=2m
Подставляем значение x01 в функцию:
y01=–х2+4mх–m=–(2m)2+4m(2m)–m=–4m2+8m2–m=4m2–m
Для второй функции у=х2+2mх–2:
x02=-b/(2a)=-2m/(2*1)=-2m/2=-m
Подставляем значение x02 в функцию:
y02=х2+2mх–2=(-m)2+2m(-m)–2=m2-2m2–2=-m2–2
Рассмотрим два варианта, когда оба значения больше нуля и, когда меньше нуля.
1) Когда обе вершины над осью Х:
 y01=4m2–m>0
y01=4m2–m>0
y02=-m2–2>0
 4m2>m
4m2>m
-2>m2
Посмотрим на второе неравенство -2>m2 - это неравенство не имеет решений, так как квадрат любого числа всегда положителен и, следовательно, не может быть меньше отрицательного числа.
Следовательно вся система не имеет решений.
2) Когда обе вершины под осью Х:
 4m2–m<0
4m2–m<0
-m2–2<0 домножим левую и правую части неравенства на (-1), не забываем, что при этом меняется знак неравенства на противоположный
 m(4m-1)<0
m(4m-1)<0
m2+2>0
Чтобы решить первое неравенство найдем корни уравнения m(4m-1)=0
m1=0
m2=1/4=0,25
Первое неравенство верно на диапазоне (0; 0,25)
Решим второе неравенство:
m2+2>0
m2>-2
Второе неравенство верно при любых m, т.к. квадрат любого числа всегда больше нуля.
Следовательно, решение данного неравенства диапазон (-∞;+∞)
Пересекаем решения обоих неравенств, получаем решение системы неравенств:
m⊂(0; 0,25)
Ответ: m⊂(0; 0,25)
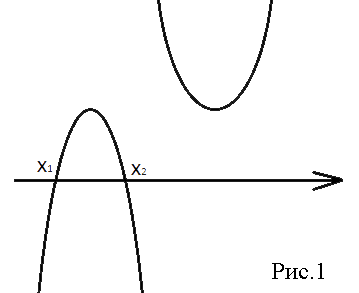
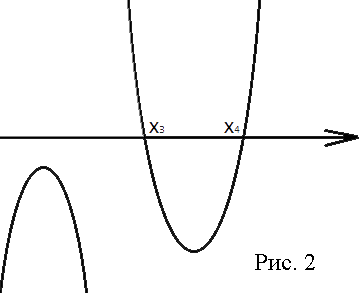
 16m2-4m>0
16m2-4m>0 4m2-m>0
4m2-m>0 16m2-4m<0
16m2-4m<0 4m2-m<0
4m2-m<0 m(4m-1)<0
m(4m-1)<0Поделитесь решением
Присоединяйтесь к нам...
В течение августа помидоры подешевели на 40%, а затем в течение сентября подорожали на 70%. Какая цена больше: в начале августа или в конце сентября – и на сколько процентов?
Упростите выражение 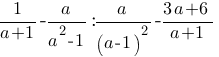
Найдите значение выражения 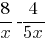 при x=-1,5.
при x=-1,5.
Сравните числа √
Найдите значение выражения 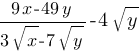 , если √
, если √
Комментарии:
(2022-12-04 18:05:04) : 0B1A91
(2015-10-30 19:05:44) Администратор: Татьяна, отличный вариант, спасибо. Я решил опубликовать его.
(2015-10-23 22:56:09) татьяна: я решила,найдя у вершин,а после методом интервалов нашла промежутки одинакового знака
(2015-02-04 17:50:58) Администратор: Даша, чтобы график первой функции пересекал ось х, уравнение должно иметь корни, следовательно, дискриминант этого уравнения ДОЛЖЕН быть больше нуля. А дискриминант второго, соответственно, меньше нуля. Т.е. мы сами задаем это условие.
(2015-02-04 17:18:49) : D1=(4m)2-4(-1)(-m)=16m2-4m>0. вот здесь
(2015-02-04 17:00:18) ДАША : в 1
(2015-02-03 19:16:58) Администратор: Даша, поясните, пожалуйста, о каком случае идет речь? о 1) или о 2)?
(2015-02-03 19:08:57) Даша: Почему 16m2-4m больше ноля а не меньше ?
(2014-11-06 22:16:06) Администратор: Исправлено!
(2014-11-06 14:40:03) : неверно по одну сторону а не по разные