
 В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
По условию задачи треугольник ABC -
равнобедренный.
BM является не только
медианой, но и
высотой (по
третьему свойству равнобедренного треугольника).
Следовательно:
1) AM=MC=AC/2=24/2=12
2) Треугольник ABM
прямоугольный.
Тогда, по
теореме Пифагора:
AB2=BM2+AM2
372=BM2+122
1369=BM2+144
BM2=1225
BM=35
Ответ: 35
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
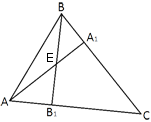 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
 Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Комментарии: