
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ716 –Є–Ј 1087 |
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ BE –Є –Љ–µ–і–Є–∞–љ–∞ AD –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О –і–ї–Є–љ—Г, —А–∞–≤–љ—Г—О 136. –Э–∞–є–і–Є—В–µ —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ BE –Є –Љ–µ–і–Є–∞–љ–∞ AD –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О –і–ї–Є–љ—Г, —А–∞–≤–љ—Г—О 136. –Э–∞–є–і–Є—В–µ —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т–∞—А–Є–∞–љ—В вДЦ1
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABD.
BO –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ AD (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —В.–µ. ∠BOD=∠BOA=90¬∞.
∠ABO=∠DBO (—В.–Ї. BE -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞).
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABO –Є DBO —А–∞–≤–љ—Л (–њ–Њ
–≤—В–Њ—А–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AB=BD.
–Ґ.–µ. —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABD -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
BO -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Є
–Љ–µ–і–Є–∞–љ–∞, –Є
–≤—Л—Б–Њ—В–∞ (–њ–Њ —В—А–µ—В—М–µ–Љ—Г
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AO=OD=AD/2=136/2=68.
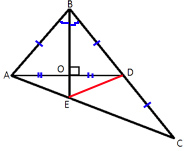 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї ED –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BEC.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї ED –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BEC.
ED -
–Љ–µ–і–Є–∞–љ–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–∞–Ї –Ї–∞–Ї –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г BC –њ–Њ–њ–Њ–ї–∞–Љ.
–Я–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ EDC –Є EDB —А–∞–≤–љ—Л (–њ–Њ –≤—В–Њ—А–Њ–Љ—Г
—Б–≤–Њ–є—Б—В–≤—Г –Љ–µ–і–Є–∞–љ—Л). SEDC=SEDB=(BE*OD)/2=(136*68)/2=68*68=4624
SABE=(BE*AO)/2=(136*68)/2=4624
–Ґ.–µ. SABE=SEDC=SEDB=4624
–Ґ–Њ–≥–і–∞, SAB–°=3*4624=13872
AD -
–Љ–µ–і–Є–∞–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC (–њ–Њ —Г—Б–ї–Њ–≤–Є—О), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –і–µ–ї–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ –і–≤–∞ —А–∞–≤–љ—Л—Е –њ–Њ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABD –Є ACD (–њ–Њ
–≤—В–Њ—А–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г –Љ–µ–і–Є–∞–љ—Л).
SABD=(AD*BO)/2=SABC/2
(136*BO)/2=13872/2
BO=13872/136=102
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABO, –Њ–љ
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ–≥–і–∞ –њ—А–Є–Љ–µ–љ–Є–Љ
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=BO2+AO2
AB2=1022+682
AB2=10404+4624=15028
AB=√
BC=2AB=2*34√
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AOE.
OE=BE-BO=136-102=34
–Ґ–∞–Ї –Ї–∞–Ї —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —В–Њ–ґ–µ
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ –Љ–Њ–ґ–љ–Њ –њ—А–Є–Љ–µ–љ–Є—В—М
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AE2=AO2+OE2
AE2=682+342=4624+1156=5780
AE=√
–Ґ–∞–Ї –Ї–∞–Ї BE -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞, —В–Њ –Є—Б–њ–Њ–ї—М–Ј—Г—П –µ–µ
–њ–µ—А–≤–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ –Ј–∞–њ–Є—И–µ–Љ:
BC/AB=CE/AE
68√
2=CE/(34√
CE=68√
AC=AE+CE=34√
–Ю—В–≤–µ—В: AB=34√
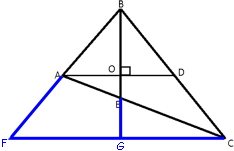 –Я—А–Њ–≤–µ–і—С–Љ —З–µ—А–µ–Ј —В–Њ—З–Ї—Г C –њ—А—П–Љ—Г—О, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Г—О AD. –Я—А–Њ–і–ї–Є–Љ BA –Є BE –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б —Н—В–Њ–є –њ—А—П–Љ–Њ–є –≤ —В–Њ—З–Ї–∞—Е F –Є G —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Я—А–Њ–≤–µ–і—С–Љ —З–µ—А–µ–Ј —В–Њ—З–Ї—Г C –њ—А—П–Љ—Г—О, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Г—О AD. –Я—А–Њ–і–ї–Є–Љ BA –Є BE –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б —Н—В–Њ–є –њ—А—П–Љ–Њ–є –≤ —В–Њ—З–Ї–∞—Е F –Є G —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –¶–µ–љ—В—А—Л –≤–њ–Є—Б–∞–љ–љ–Њ–є –Є –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–µ–є —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б–Њ–≤–њ–∞–і–∞—О—В.
2) –°—Г—Й–µ—Б—В–≤—Г–µ—В –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ, –Ї–Њ—В–Њ—А—Л–є –љ–µ —П–≤–ї—П–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ.
3) –°—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ —В—Г–њ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 180¬∞.
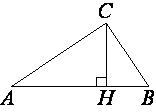 –Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Ї–∞—В–µ—В AC=35, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 14√
–Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Ї–∞—В–µ—В AC=35, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 14√
 –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –≤ —В–Њ—З–Ї–∞—Е K –Є P —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –≤–µ—А—И–Є–љ—Л B –Є C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ KP, –µ—Б–ї–Є AK=18, –∞ —Б—В–Њ—А–Њ–љ–∞ AC –≤ 1,2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л BC.
–Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –≤ —В–Њ—З–Ї–∞—Е K –Є P —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –Є –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –≤–µ—А—И–Є–љ—Л B –Є C. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –Њ—В—А–µ–Ј–Ї–∞ KP, –µ—Б–ї–Є AK=18, –∞ —Б—В–Њ—А–Њ–љ–∞ AC –≤ 1,2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —Б—В–Њ—А–Њ–љ—Л BC.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 32, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 32, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є—П AD –Є BC —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 33 –Є 11,
–∞ —Б—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є AD —А–∞–≤–љ–∞ 90¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї–Є A –Є B –Є –Ї–∞—Б–∞—О—Й–µ–є—Б—П –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AB=20.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є—П AD –Є BC —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 33 –Є 11,
–∞ —Б—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є AD —А–∞–≤–љ–∞ 90¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї–Є A –Є B –Є –Ї–∞—Б–∞—О—Й–µ–є—Б—П –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AB=20.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: