
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ829 –Є–Ј 1087 |
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є—П AD –Є BC —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 33 –Є 11,
–∞ —Б—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є AD —А–∞–≤–љ–∞ 90¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї–Є A –Є B –Є –Ї–∞—Б–∞—О—Й–µ–є—Б—П –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AB=20.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD –Њ—Б–љ–Њ–≤–∞–љ–Є—П AD –Є BC —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 33 –Є 11,
–∞ —Б—Г–Љ–Љ–∞ —Г–≥–ї–Њ–≤ –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є AD —А–∞–≤–љ–∞ 90¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ—А–Њ—Е–Њ–і—П—Й–µ–є —З–µ—А–µ–Ј —В–Њ—З–Ї–Є A –Є B –Є –Ї–∞—Б–∞—О—Й–µ–є—Б—П –њ—А—П–Љ–Њ–є CD, –µ—Б–ї–Є AB=20.
–Я—А–Њ–і–ї–Є–Љ —Б—В–Њ—А–Њ–љ—Л AB –Є CD –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і—А—Г–≥ —Б –і—А—Г–≥–Њ–Љ.
 –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AED.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AED.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞:
180¬∞=∠EDA+∠DAE+∠AED
180¬∞=90¬∞+∠AED
∠AED=90¬∞
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AED -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AED –Є BEC.
∠AED - –Њ–±—Й–Є–є
∠EBC=∠EAD (—В.–Ї. —Н—В–Њ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ—Л–µ —Г–≥–ї—Л)
–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є AED –Є BEC
–њ–Њ–і–Њ–±–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г –њ–Њ–і–Њ–±–Є—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–Ґ–Њ–≥–і–∞ –њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–Њ–і–Њ–±–Є—П:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
33/11=(20+BE)/BE
3=(20+BE)/BE
3BE=20+BE
2BE=20
BE=10
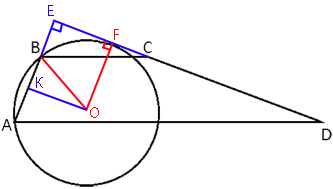 –Ґ–Њ—З–Ї–∞ F - —В–Њ—З–Ї–∞ –Ї–∞—Б–∞–љ–Є—П –њ—А—П–Љ–Њ–є CD –Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–Ґ–Њ—З–Ї–∞ F - —В–Њ—З–Ї–∞ –Ї–∞—Б–∞–љ–Є—П –њ—А—П–Љ–Њ–є CD –Є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Є —Б–µ–Ї—Г—Й–µ–є:
EF2=BE*AE=BE*(AB+BE)=10(20+10)=300
EF=√
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї EOK.
–Ю - —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є
OB - —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є
OK -
—Б–µ—А–µ–і–Є–љ–љ—Л–є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А –Ї
—Е–Њ—А–і–µ AB (
—В—А–µ—В—М–µ —Б–≤–Њ–є—Б—В–≤–Њ —Е–Њ—А–і—Л)
OK=EF (—В.–Ї. KEFO -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї)
KB=AB/2 (—В.–Ї. OK -
—Б–µ—А–µ–і–Є–љ–љ—Л–є –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А)
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
OB2=OK2+KB2
OB2=(√
OB2=300+100=400
OB=20=R
–Ю—В–≤–µ—В: 20
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –њ—А–Њ–≤–µ–і–µ–љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М AC. –Ґ–Њ—З–Ї–∞ O —П–≤–ї—П–µ—В—Б—П —Ж–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC. –†–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —В–Њ—З–Ї–Є O –і–Њ —В–Њ—З–Ї–Є A –Є –њ—А—П–Љ—Л—Е AD –Є AC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л 5, 4 –Є 3. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD –њ—А–Њ–≤–µ–і–µ–љ–∞ –і–Є–∞–≥–Њ–љ–∞–ї—М AC. –Ґ–Њ—З–Ї–∞ O —П–≤–ї—П–µ—В—Б—П —Ж–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABC. –†–∞—Б—Б—В–Њ—П–љ–Є—П –Њ—В —В–Њ—З–Ї–Є O –і–Њ —В–Њ—З–Ї–Є A –Є –њ—А—П–Љ—Л—Е AD –Є AC —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л 5, 4 –Є 3. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD.
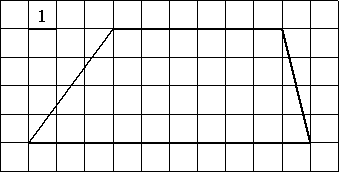 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
 –Т —В—А–∞–њ–µ—Ж–Є—О, —Б—Г–Љ–Љ–∞ –і–ї–Є–љ –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ 16, –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є.
–Т —В—А–∞–њ–µ—Ж–Є—О, —Б—Г–Љ–Љ–∞ –і–ї–Є–љ –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ 16, –≤–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є.
 –Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 5 –Є 45, BD=15. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є BDA –њ–Њ–і–Њ–±–љ—Л.
–Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 5 –Є 45, BD=15. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є BDA –њ–Њ–і–Њ–±–љ—Л.
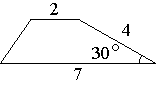 –С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 4, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ 30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 7.
–С–Њ–Ї–Њ–≤–∞—П —Б—В–Њ—А–Њ–љ–∞ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 4, –∞ –Њ–і–Є–љ –Є–Ј –њ—А–Є–ї–µ–≥–∞—О—Й–Є—Е –Ї –љ–µ–є —Г–≥–ї–Њ–≤ —А–∞–≤–µ–љ 30¬∞. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –µ—Б–ї–Є –µ—С –Њ—Б–љ–Њ–≤–∞–љ–Є—П —А–∞–≤–љ—Л 2 –Є 7.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: