
 В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
Площадь трапеции вычисляется по формуле: произведение полусуммы оснований и высоты.
Т.е. для трапеции ABCD можем записать:
SABCD=h*(AD+BC)/2
84=h*(4+3)/2
168=7h
h=24
Для трапеции BCNM:
SBCNM=hBCNM*(MN+BC)/2
MN - это средняя линия, значит длина равна полусумме оснований:
MN=(AD+BC)/2=(4+3)/2=3,5
Высота трапеции BCNM равна половине высоты трапеции ABCD (по
теореме Фалеса), тогда:
SBCNM=hBCNM*(MN+BC)/2=(h/2)*(3,5+BC)/2=(24/2)*(3,5+3)/2=12*3,25=39
Ответ: 39
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
 естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
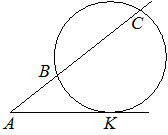 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
 Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
Площадь ромба равна 30, а периметр равен 24. Найдите высоту ромба.
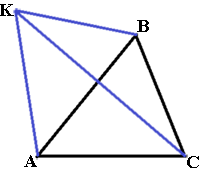 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
Комментарии: