
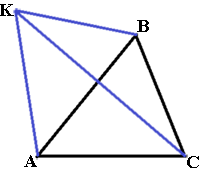
 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
По условию задачи ∠KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 2√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. ∠KAC=∠ABC. ∠ACK не равен ∠ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому ∠ACK = ∠BAC. Следовательно, ∠AKC=∠ACB => cos(∠AKC)=cos(∠ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(∠ACB).
(√
5=4*2+1-4*√
5-9=-4*√
4=4*√
cos(∠ACB)=1/√
Для удобства домножим числитель и знаменатель на √
cos(∠ACB)=√
cos(∠AKC)=cos(∠ACB)=√
Ответ: √
Поделитесь решением
Присоединяйтесь к нам...
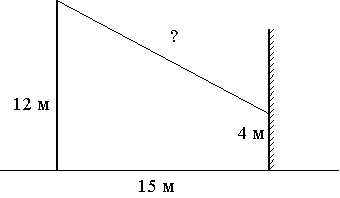 От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода.
 Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
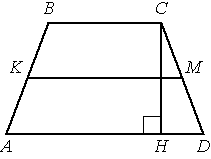 В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
 В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
Комментарии:
(2017-03-25 19:37:07) Администратор: Евгения, я добавил в решение пару строк, чтобы стало понятней.
(2017-03-25 12:34:31) Евгения: Добрый день, как в знаменателе в ответе появилась 2? Спасибо