
 Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 5. Точка E – середина стороны AD. Найдите площадь трапеции AECB.
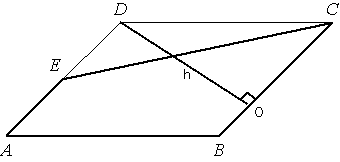 Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Sпараллелограмма=BC*h=5
А площадь
трапеции равна произведению полусуммы оснований на высоту.
Sтрапеции=h*(BC+AE)/2.
AE=AD/2 (по условию задачи).
AD=BC (по
свойству параллелограмма).
Следовательно AE=BC/2.
Тогда Sтрапеции=h*(BC+BC/2)/2 = h*(3*BC/2)/2 = h*3*BC/4=h*BC*3/4 = Sпарал-ма*3/4=5*3/4=3,75.
Ответ: Sтрапеции=3,75.
Поделитесь решением
Присоединяйтесь к нам...
 Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Синус острого угла A треугольника ABC равен  . Найдите CosA.
. Найдите CosA.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
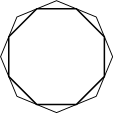 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Комментарии:
(2015-05-25 21:18:55) Администратор: BC+BC/2=(2BC)/2+BC/2=(3BC)/2
(2015-05-25 19:09:28) : а откуда вы взял 3 в S трапеции
(2015-05-25 19:09:05) : 543