Синус острого угла A треугольника ABC равен 
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться
основной тригонометрической формулой:
sin2A+cos2A=1
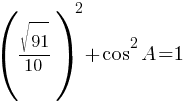
По
второму правилу действий со степенями:
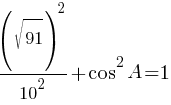
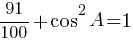
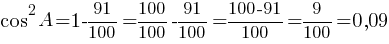
cosA=√0,09=0,3
Ответ: 0,3
Поделитесь решением
Присоединяйтесь к нам...
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
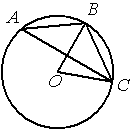Точка О – центр окружности, /BOC=70° (см. рисунок). Найдите величину угла BAC (в градусах).
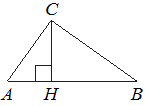На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
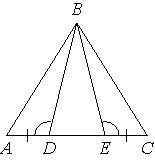На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: