В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
Рассмотрим треугольник ABL.
∠BLA=180°-∠ALC=180°-52°=128° (т.к. это
смежные углы)
По
теореме о сумме углов треугольника:
180°=∠ABC+∠BLA+∠LAB=13°+128°+∠LAB
∠LAB=180°-13°-128°=39°
Рассмотрим треугольник ALC.
∠LAC=∠LAB=39° (т.к. AL -
биссектриса)
По
теореме о сумме углов треугольника:
180°=∠ALC+∠ACB+∠LAC=52°+∠ACB+39°
∠ACB=180°-52°-39°=89°
Ответ: 89
Поделитесь решением
Присоединяйтесь к нам...
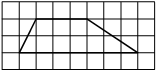На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
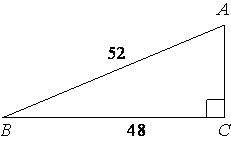Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
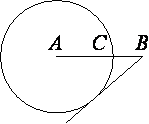На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: