
 Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 10,52+362=110,25+1296=1406,25
Тогда длина гипотенузы равна √
Т.к. ступеней 20 шт., то расстояние от А до В составляет 20*37,5=750 см, что равняется 7,5 м.
Ответ: 7,5
Поделитесь решением
Присоединяйтесь к нам...
 Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
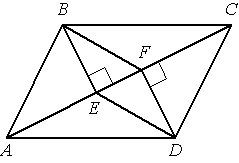 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
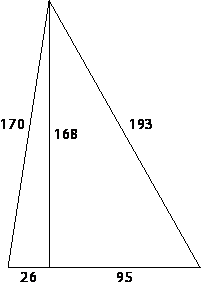 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
Комментарии: