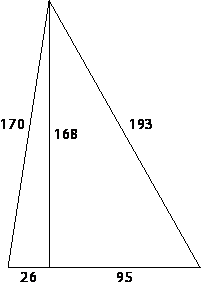Найдите площадь треугольника, изображённого на рисунке.
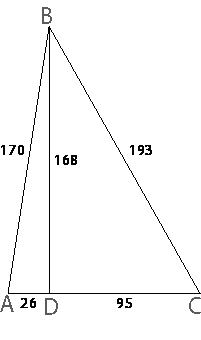Обозначим ключевые точки как показано на рисунке.
Проверим, является ли BD
высотой данного треугольника. Если является, то треугольник ABD -
прямоугольный и к нему применима
теорема Пифагора:
AB2=AD2+BD2
1702=262+1682
28900=676+28224
28900=28900
Равенство выполняется.
Площадь треугольника равна произведению
высоты на половину стороны, к которой проведена
высота.
SABC=BD*AC/2=BD*(AD+DC)/2=168*(26+95)/2=84*121=10164
Ответ: SABC=10164
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
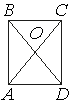Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: