
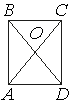
 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
BO=OD (по четвертому свойству прямоугольника).
Тогда:
BD=BO+OD=BO+BO=2*BO=2*37=74
AC=BD=74 (по второму свойству прямоугольника).
Ответ: 74
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
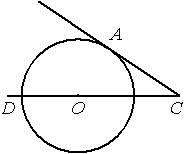 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
100°.
 Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
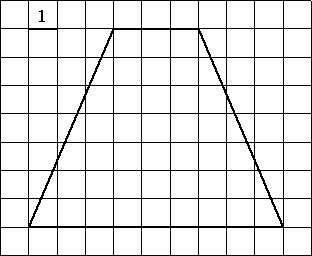 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии:
(2021-10-18 13:11:07) Администратор: Никитина Тамара, Я не помогаю решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и я ее обязательно добавлю.
(2021-02-23 08:28:10) Никитина Тамара: Диагонали осевого сечения усеченного конуса точкой пересечения делятся в отношении 2:1, считая от большего основания. Угол между диагоналями, обращенный к основаниям конуса, равен 60. Длина диагонали равна 3. Найти объем усеченного конуса.