
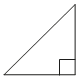
 В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
 SABC=AB*AC/2
SABC=AB*AC/2
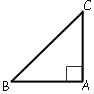
Пусть угол, равный 45° будет угол В.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=90°+45°+∠C
∠C=45°
Следовательно, по
свойству равнобедренного треугольника, треугольник ABC -
равнобедренный.
Значит AB=AC.
По
теореме Пифагора:
BC2=AB2+AC2
BC2=AB2+AB2
822=2AB2
6724=2AB2
AB2=3362
SABC=AB*AC/2
SABC=AB2/2=3362/2=1681
Ответ: SABC=1681
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
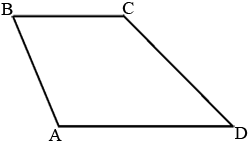 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
Комментарии: