
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
 Введем обозначения ключевых точек и проведем высоту как показано на рисунке.
Введем обозначения ключевых точек и проведем высоту как показано на рисунке.
ABEC - квадрат, так как все углы прямые и все стороны равны.
Т.е. BE=EC=AB=54
tgα=BE/ED=2/9 (по
определению).
54/ED=2/9
ED=54*9/2=27*9=243
CD=CE+ED=54+243=297
Ответ: 297
Поделитесь решением
Присоединяйтесь к нам...
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
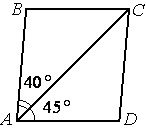 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
 К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Комментарии: