
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
По третьему свойству вписанной окружности, радиус вписанной окружности равен:
r=S/p, где S - площадь треугольника, а p - полупериметр.
p=50/2=25
S=r*p=4*25=100
Ответ: 100
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, BC=5, AC=3.
В треугольнике ABC угол C равен 90°, BC=5, AC=3.
Найдите tgB.
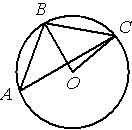 Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
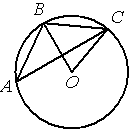 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Синус острого угла A треугольника ABC равен 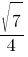 . Найдите CosA.
. Найдите CosA.
Комментарии:
(2024-04-15 22:12:16) : Периметр треугольника равен 18, одна из сторон равна 7, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
(2024-04-15 22:10:49) амина: Периметр треугольника равен 18, одна из сторон равна 7, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.