
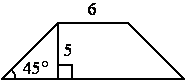 В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
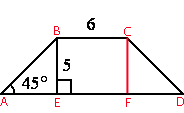 Проведем
высоту CF.
Проведем
высоту CF.
Рассмотрим треугольники ABE и DCF.
∠BAE=∠CDF=45° (по
свойству равнобедренной трапеции).
∠BEA=∠CFD=90° (так как BE и CF -
высоты).
Используя
теорему о сумме углов треугольника, получаем, что:
∠EBA=∠FCD
AB=CD (по
определению равнобедренной трапеции).
Следовательно, данные треугольники равны (по
второму признаку равенства треугольников).
Значит, AE=FD.
Рассмотрим треугольник ABE.
По
определению tg∠BAE=BE/AE
tg45°=5/AE=1 (по
таблице)
AE=5
EF=BC=6 (так как BCFE -
прямоугольник)
AD=AE+EF+FD=5+6+5=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
 Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
 В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 2 м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Комментарии: