Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
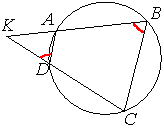По условию задачи, четырехугольник вписан в окружность, следовательно, сумма его противоположных углов равна 180° (по
свойству описанной окружности).
Т.е. ∠ABC+∠ADC=180°
∠ADC=180°-∠ABC
∠KDA - является
смежным углу ADC, следовательно:
∠KDA+∠ADC=180°
Подставляем значение угла ADC:
∠KDA+(180°-∠ABC)=180°
∠KDA+180°-∠ABC=180°
∠KDA+180°-180°=∠ABC
∠KDA=∠ABC
Т.е. эти углы равны.
Рассмотрим треугольникик AKD и BKC.
∠BKC - общий.
∠KDA=∠ABC, это мы определили ранее.
Следовательно, данные треугольники
подобны (по
первому признаку подобия).
Тогда:
BK/DK=BC/AD
AD=(DK*BC)/BK=(15*12)/20=(3*12)/4=3*3=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
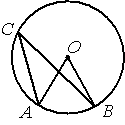Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Стороны AC, AB, BC треугольника ABC равны 3√
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: