
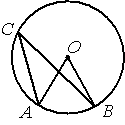
 Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=70°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 70°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 70/2=35.
Ответ: /ACB=35°.
Поделитесь решением
Присоединяйтесь к нам...
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.
 В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
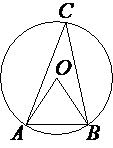 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
 Площадь прямоугольного треугольника равна 32√
Площадь прямоугольного треугольника равна 32√
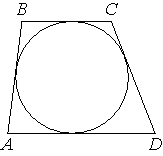 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Комментарии: