
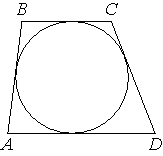 Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Так как в трапецию вписана
окружность, то:
AD+BC=AВ+CD (по четвертому свойству трапеции).
AD+13=14+22
AD=14+22-13=23
Ответ: 23
Поделитесь решением
Присоединяйтесь к нам...
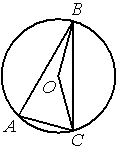 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=20, CD=48, а расстояние от центра окружности до хорды AB равно 24.
 В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
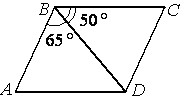 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол параллелограмма.
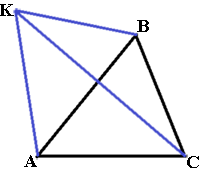 Стороны AC, AB, BC треугольника ABC равны 2√
Стороны AC, AB, BC треугольника ABC равны 2√
Комментарии:
(2019-12-25 08:18:36) С.: трапеция абсд с основаниями ад и бс вписана в окружность. так,что ад-диаметр окружности .Диагональ трапеции равна 10 см,а её площадь - 25см2.