
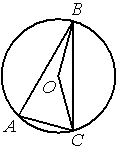
 Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
По условию ∠BOC=160°, этот угол является
центральным, соответственно дуга ВC (малая часть) тоже равна 160°.
∠BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, ∠BAC=160°/2=80°.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
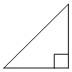 В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
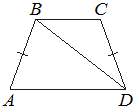 В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Комментарии: