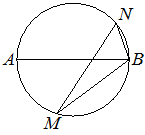
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
∠NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 69°*2=138°.
Тогда дуга NB равна 180°-138°=42°
∠NMB - тоже является
вписанным в окружность и опирается на дугу NB, следовательно он равен 42°/2=21°
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Найдите угол ABC. Ответ дайте в градусах.
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: