Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Пусть а и b -
катеты треугольника, с - гипотенуза.
Площадь
прямоугольного треугольника равна половине произведения катетов.
S=ab/2=32√
ab=64√
a=64√
По
теореме Пифагора:
c2=a2+b2
162=(64√
256b2=642*3+b4
b4-256b2+12288=0
Обозначим b2=t
t2-256t+12288=0
Решим это
квадратное уравнение:
D=(-256)2-4*12288=65536-49152=16384
√
t1=(-(-256)+128)/2=192
t2=(-(-256)-128)/2=64
Рассмотрим оба случая:
1) t=192=b2
b=√
По
определению, cosα=b/c=8√
α=30° (по
таблице)
По
теореме о сумме углов треугольника, второй острый угол равен 180°-90°-30°=60°
2) t=64=b2
b=8
По
определению, cosα=b/c=8/16=1/2
α=60° (по
таблице)
По
теореме о сумме углов треугольника, второй острый угол равен 180°-90°-60°=30°
Ответ: 30° и 60°
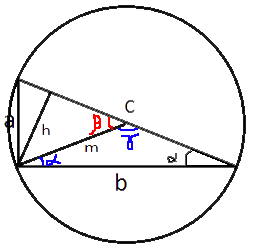Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.Поделитесь решением
Присоединяйтесь к нам...
Катеты прямоугольного треугольника равны 3√
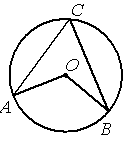Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=57°. Найдите величину угла BOC. Ответ дайте в градусах.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-05-15 11:36:55) Алекс: Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36,а его площадь равна 162 корня из 3
(2023-05-15 11:36:10) Алекс : Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36,а его площадь равна 162 корня из 3