
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 47°*2=94°.
Тогда дуга NB равна 180°-94°=86°
/NMB - тоже
вписанный в окружность, следовательно он равен 86°/2=43°
Ответ: 43
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
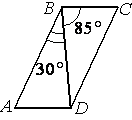 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
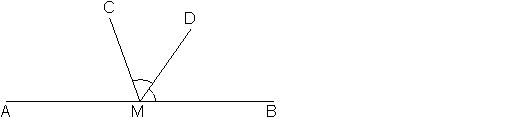 На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
На прямой AB взята точка M. Луч MD – биссектриса угла CMB. Известно, что /DMC=60°. Найдите угол CMA. Ответ дайте в градусах.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Комментарии: