
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 64°*2=128°.
Тогда дуга NB равна 180°-128°=52°
/NMB - тоже
вписанный в окружность, следовательно он равен 52°/2=26°
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
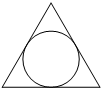 Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Комментарии: