Последовательность задана формулой an=40/(n+1). Сколько членов этой последовательности больше 2?
Для решения этой задачи надо решить неравенство:
40/(n+1)>2
40>2(n+1)
20>n+1
19>n
Так как в
арифметической прогрессии n - натуральное, то нас интересуют только целые положительные числа, т.е. от 1 до 18. Таким образом получается, что при n=1, 2, 3,..., 18, an будет больше 2.
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Выписаны первые три члена геометрической прогрессии:
125; -100; 80; …
Найдите её пятый член.
Геометрическая прогрессия задана условием bn=64,5(-2)n. Найдите b6.
Выписаны первые несколько членов арифметической прогрессии: 6; 8; 10; … Найдите сумму первых шестидесяти её членов.
В геометрической прогрессии сумма первого и второго членов равна 40, а сумма второго и третьего членов равна 120. Найдите первые три члена этой прогрессии.
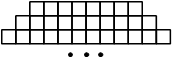Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 117-й строке?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: