
 Катеты прямоугольного треугольника равны 4√
Катеты прямоугольного треугольника равны 4√
 Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=22+(4√
AB2=4+16*6=100
AB=10
Меньший угол лежит напротив меньшей стороны, 2<4√
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
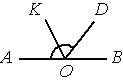 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
 На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
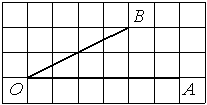 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
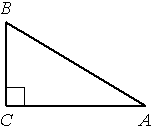 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
Комментарии: