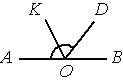
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
∠AOD=180°-∠DOB=180°-52°=128° (так как ∠AOB - развернутый, т.е. равен 180°).
Так как OK - биссектриса, то ∠DOK=∠AOD/2=128°/2=64°
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
Площадь равнобедренного треугольника равна 196√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: