
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Рассмотрим треугольники ABC и MBN.
∠ABC - общий
∠BAC=∠BMN (соответственные углы)
Следовательно, по первому признаку подобия, данные треугольники
подобны (по двум углам).
Поэтому мы можем записать пропорцию соотношения сторон
подобных треугольников:
MN/AC=MB/AB
24/44=MB/66
MB=24*66/44=24*6/4=6*6=36
AM=AB-MB=66-36=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
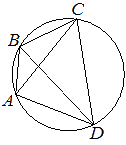 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
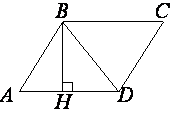 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
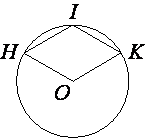 Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
 В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
Комментарии: