
 В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 30, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=30
По
определению средней линии трапеции: m=(BC+AD)/2=30/2=15
Ответ: m=15
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
 Катеты прямоугольного треугольника равны √
Катеты прямоугольного треугольника равны √
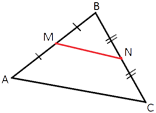 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Комментарии: