
Решите уравнение (x2-9)2+(x2+x-6)2=0
Вариант №1
Заметим, что в левой части уравнения складываются два положительных выражения (т.к. скобки в квадрате), а сумма этих положительных выражений равна нулю.
Такое возможно тогда и только тогда, когда оба выражения равны нулю:
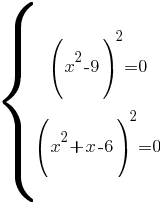
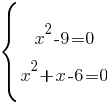
Теперь достаточно решить оба этих уравнения и корни, которые совпадут для обоих уравнений, и будут решением первоначального уравнения.
1) x2-9=0
Можно решить это
квадратное уравнение через
дискриминант, но в данном случае удобней воспользоваться формулой
разность квадратов:
x2-32=0
(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю:
x-3=0 => x1=3
x+3=0 => x2=-3
2) x2+x-6=0
Решим это
квадратное уравнение через
дискриминант:
D=12-4*1*(-6)=1+24=25
x1=(-1+5)/(2*1)=4/2=2
x2=(-1-5)/(2*1)=-6/2=-3,
Для обоих уравнений совпал корень x=-3.
Ответ: -3
Поделитесь решением
Присоединяйтесь к нам...
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 33 км/ч, а вторую половину пути проехал со скоростью на 22 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Решите неравенство 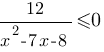
Укажите неравенство, решение которого изображено на рисунке.

1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Найдите корень уравнения 4(x-8)=-5.
Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 4 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой — со скоростью 4,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Комментарии:
(2017-06-03 18:57:14) Администратор: Виктория, противоречия не было бы (x-3)2+(x-3)2=0, корень этого уравнения x=3.
(2017-06-02 11:37:43) Виктория: А в каком случае не было бы противоречия?
(2014-05-28 22:13:16) Администратор: Таня, потому, что у второго уравнения (x-3)2+(x-2)2=0 корней нет. Мы же там получили противоречие. Поэтому подходит корень только от первого уравнения.
(2014-05-28 12:49:50) Таня : а почему записали только один ответ?
(2014-04-29 18:13:12) Администратор: Людмила, конечно, оформлять можно, кому как нравится. Главное, чтобы было понятно, как решать подобные задачи.
(2014-04-29 16:15:49) людмила: можно сразу написать систему и каждое слагаемое приравнять 0