
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 33 км/ч, а вторую половину пути проехал со скоростью на 22 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Введем обозначения:
v1 - скорость первого автомобилиста.
S - длина пути от А до В.
Тогда:
S/v1 - время в пути первого автомобилиста.
S/2 - половина пути.
S/(2*33) - время второго автомобилиста на первой половине пути.
v1+22 - скорость второго автомобилиста на второй половине пути.
S/(2*(v1+22)) - время, за которое второй автомобилист проехал вторую половину пути.
Так как автомобилисты одновременно прибыли в пункт В, то суммарное время в пути у них одинаковое:

Немного упростим выражение, в правой части уравнения вынесем S за скобку.
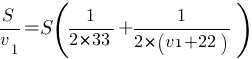
Сократим S:
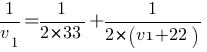
В правой части приведем дроби к общему знаменателю:
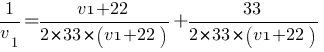
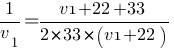

66(v1+22)=v1(v1+55)
66v1+66*22=v12+55v1
0=v12+55v1-66v1-66*22
0=v12-11v1-1452
Решим это квадратное уравнение через дискриминант:
D=(-11)2-4*1*(-1452)=121+5808=5929
v1-1=(-(-11)+77)/(2*1)=(11+77)/2=88/2=44
v1-2=(-(-11)-77)/(2*1)=(11-77)/2=-66/2=-33
Так как скорость отрицательной быть не может, то v1=44 км/ч.
Ответ: 44
Поделитесь решением
Присоединяйтесь к нам...
Укажите решение неравенства 4x-4≥9x+6.
1) [-0,4;+∞)
2) (-∞;-2]
3) [-2;+∞)
4) (-∞;-0,4]
 На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
На рисунке изображены графики функций y=6-x2 и y=5x. Вычислите абсциссу точки B.
Решите систему уравнений 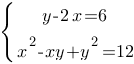
Решите уравнение -2x2+x+7=-x2+5x+(-2-x2).
Найдите корень уравнения 4(x-8)=-5.
Комментарии: