
В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника.
По
теореме о сумме углов треугольника можно вычислить третий угол, он равен 180°-90°-45°=45°.
Следовательно, этот треугольник
равнобедренный (по первому
свойству).
Т.е. катеты этого треугольника равны.
Площадь
прямоугольного треугольника = ab/2, где а и b - катеты. Тогда:
Sтреугольника=35*35/2=612,5
Ответ: Sтреугольника=612,5
Поделитесь решением
Присоединяйтесь к нам...
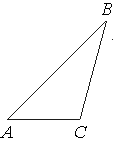 В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=6√
 Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=18, а сторона AC в 1,2 раза больше стороны BC.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
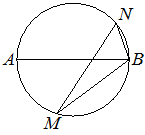 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Комментарии: