
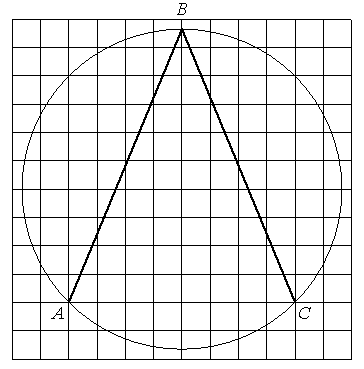
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
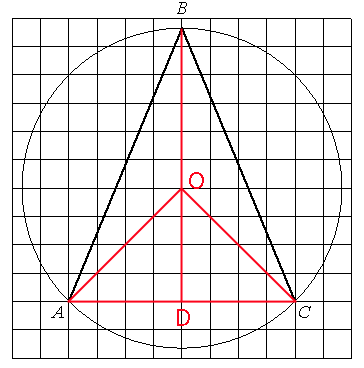 Проведем отрезки как показано на рисунке. Точка О - центр окружности
Проведем отрезки как показано на рисунке. Точка О - центр окружности
Рассмотрим треугольник AOD.
Данный треугольник
прямоугольный, так как ∠ODA=90°
AD=OD=4, следовательно треугольник AOD -
равнобедренный.
По
теореме о сумме углов треугольника:
180°=∠ODA+∠DAO+∠AOD
180°=90°+∠DAO+∠AOD
90°=∠DAO+∠AOD
А так как ∠DAO=∠AOD (по
свойству равнобедренного треугольника), то:
∠DAO=∠AOD=90°/2=45°.
Рассмотрим треугольники AOD и COD.
AD=CD=4
OD=4 - общая сторона.
∠ODA=∠ODC=90°
Тогда, по
первому признаку равенства треугольников, данные треугольники равны.
Следовательно, ∠AOD=∠COD=45°
∠AOC=∠AOD+∠COD=45°+45°=90°
∠AOC - является
центральным для окружности, следовательно градусная мера дуги, на которую опирается этот угол тоже равна 90°.
∠ABC - является
вписанным в окружность и опирается на ту же дугу. Следовательно, по
свойству угла, он равен половине градусной меры дуги. ∠ABC=90°/2=45°.
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
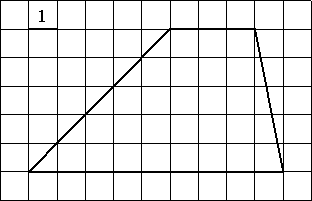 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
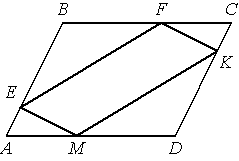 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
 В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
 Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Комментарии: