
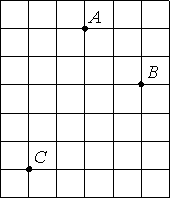
 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
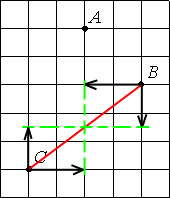 Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 2 клетки вправо и на 1,5 клетки вверх.
Относительно точки В на 2 клетки влево и на 1,5 клетки вниз.
Тогда очевидно, что расстояние от точки А до середины ВС равно 3,5 клетки, т.е. 3,5см
Ответ: 3,5
Поделитесь решением
Присоединяйтесь к нам...
 Один из углов параллелограмма равен 111°. Найдите меньший угол этого параллелограмма. Ответ дайте
в градусах.
Один из углов параллелограмма равен 111°. Найдите меньший угол этого параллелограмма. Ответ дайте
в градусах.
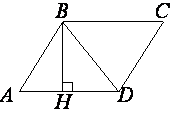 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=6 и HD=75. Диагональ параллелограмма BD равна 85. Найдите площадь параллелограмма.
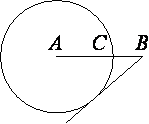 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
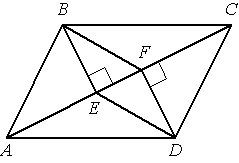 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
 Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Комментарии:
(2017-02-19 17:24:55) Даниил: Спасибо за труды автору, помог!
(2014-05-31 22:06:34) Администратор: ТАНЮШКА, очень рад за Вас, очень рад, что не напрасно создал сайт. Спасибо Вам, что поделились радостью, очень приятно!
(2014-05-31 21:12:02) ТАНЮШКА: Спасибо вам за решение. Благодаря вашему сайту, я смогла решить подобную задачу на реальном гиа(ОГЭ)!