Решите уравнение (x-4)(x-5)(x-6)=(x-2)(x-5)(x-6).
(x-4)(x-5)(x-6)=(x-2)(x-5)(x-6)
(x-4)(x-5)(x-6)-(x-2)(x-5)(x-6)=0
Выносим за скобки (x-5)(x-6):
(x-5)(x-6)((x-4)-(x-2))=0
(x-5)(x-6)(x-4-x+2)=0
(x-5)(x-6)(-2)=0 |:(-2)
(x-5)(x-6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x-5=0 => x1=5
2) x-6=0 => x2=6
Ответ: x1=5, x2=6.
Поделитесь решением
Присоединяйтесь к нам...
Закон всемирного тяготения можно записать в виде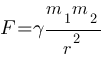 
, где F — сила притяжения между телами (в ньютонах), m1 и m2 — массы тел (в килограммах), r — расстояние между центрами масс тел (в метрах), а γ — гравитационная постоянная, равная 6,67*10-11 Н*м2/кг2. Пользуясь этой формулой, найдите массу тела m1 (в килограммах), если F=0,06003 Н, m2=6*108 кг, а r=2 м.
Постройте график функции y=|x|(x-1)-2x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
При каких значениях m вершины парабол у=–х2+4mх–m и у=х2+2mх–2 расположены по одну сторону от оси х?
Парабола проходит через точки A(0; -4), B(-1; -11), C(4; 4). Найдите координаты её вершины.
Найдите значение выражения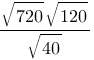 
1) 60√
2) 12√
3) 12√
4) 36√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: