Постройте график функции y=|x|(x-1)-2x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
x(x-1)-2x, при x≥0
-x(x-1)-2x, при x<0
x2-x-2x, при x≥0
-x2+x-2x, при x<0
x2-3x, при x≥0
-x2-x, при x<0
Рассмотрим каждую подфункцию:
1) x2-3x, при x≥0
Найдем корни уравнения x2-3x=0, чтобы узнать, в каких точках график пересекает ось х.
x2-3x=0
x(x-3)=0
x1=0
x2=3
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -2 | -2 | -0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -2 | -6 | -12 |
|
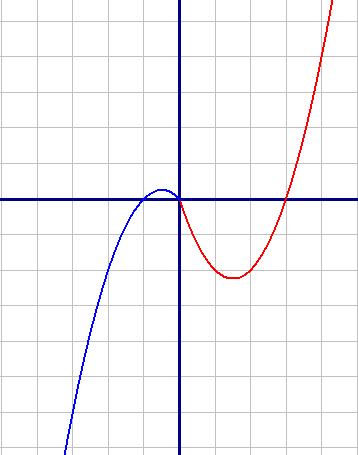
Красная кривая - это график подфункции x(x-1)-2x, при x≥0 Синяя кривая - это график подфункции -x(x-1)-2x, при x<0 Прямая y=m имеет ровно две общие точки, когда она прошодит через вершины парабол. |
|
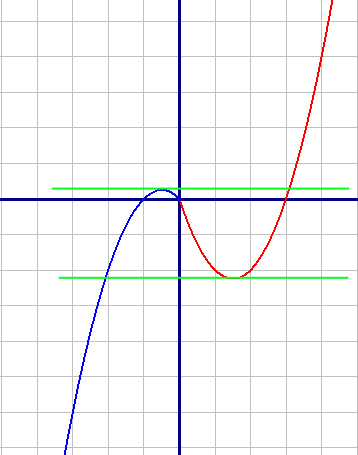
Найдем координаты y для вершин порабол: Координату x можно найти по формуле: x0=-b/(2a). Для первой подфункции: x0=-(-3)/(2*1)=1,5 y0(1,5)=1,52-3*1,5=2,25-4,5=-2,25 Для второй подфункции: x0=-(-1)/(2*(-1))=-0,5 y0(-0,5)=-(-0,5)2-(-0,5)=-0,25+0,5=0,25 |
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение (x2-25)2+(x2+3x-10)2=0.
За 3 минуты пешеход прошёл a метров. Сколько метров он пройдёт за 40 минут, если будет идти с той же скоростью? Запишите соответствующее выражение.
Решите уравнение (x+5)3=25(x+5).
Постройте график функции y=5|x-3|-x2+7x-12 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Найдите значение выражения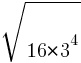 
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-10-27 21:21:41) Администратор: Ангеліна, раскройте скобки и далее уравнение очень легко решается, x=-7.
(2016-10-27 17:31:57) Ангеліна: 5 ( х - 1) - 4 ( х - 3)=0