
Решите уравнение (x2-25)2+(x2+3x-10)2=0.
(x2-25)2+(x2+3x-10)2=0
Заметим, что в уравнении сумма двух квадратов равна нулю.
Так как квадрат любого числа больше или равен нулю, то сумма таких чисел может равняться нулю только в одном случае, когда и первая скобка и вторая равны нулю, получаем систему уравнений:
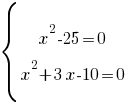
Для решения системы нужно решить каждое уравнение и совпавшие корни уравнений и будут решением системы, а так же и решением нашего первоначального уравнения.
1) x2-25=0
x2-52=0
Воспользуемся формулой разность квадратов:
(x-5)(x+5)=0
Произведение равно нулю, когда один из множителей равен нулю:
x-5=0 => x1=5
x+5=0 => x2=-5
2) x2+3x-10=0
Это квадратное уравнение решим через дискриминант:
D=32-4*1*(-10)=9+40=49
x3=(-3+7)/(2*1)=4/2=2
x4=(-3-7)/(2*1)=-10/2=-5
Совпали корни x2=x4=-5
Ответ: -5
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 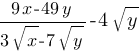 , если √
, если √
Значение какого из выражений является числом рациональным?
1) √
2) (√
3) √
4) √
Найдите значение выражения  , если √
, если √
Найдите значение выражения (1,8*10-3)(7*10-2).
Найдите значение выражения 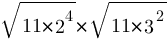
1) 1452
2) 132
3) 1584
4) 12√
Комментарии: