ОГЭ, Математика.
Геометрия: Задача №F48418
| Задача №312 из 1087
Условие задачи: | |
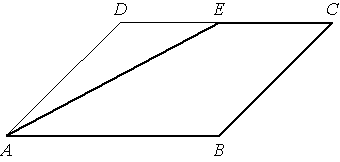 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Решение задачи:
Первый вариант решения
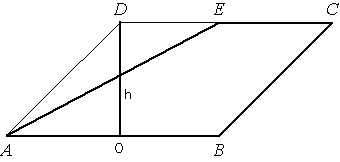
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
S
параллелограмма=AB*h=56
А площадь
трапеции равна произведению полусуммы оснований на высоту.
S
трапеции=h*(AB+EC)/2.
EC=DC/2 (по условию задачи).
DC=AB (по
свойству параллелограмма).
Следовательно EC=AB/2.
Тогда S
трапеции=h*(AB+AB/2)/2 = h*(3*AB/2)/2 = h*3*AB/4=h*AB*3/4 = S
парал-ма*3/4=56*3/4=42.
Ответ: S
трапеции=42.
Второй вариант решения задачи
Прислал пользователь Юлия
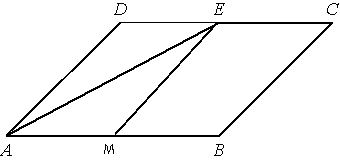
1) Отметим точку М на АB, так чтобы AM=MB
S
ADEM=S
MECB, т.к. ЕМ делит ABCD на равные части.
2) Треугольник AED равен треугольнику EAM (по
первому признаку):
/AED =
/EAM (т.к. AB||CD, AE - секущая, а эти углы -
внутренние накрест лежащие)
DЕ=AM
AE - общая сторона
3) Пусть площадь треугольника AED = х, тогда S
ABCD = 4x т.к EM делит ABCD пополам.
4x = 56
x = 14
4) S
AECB = S
ABCD - S
AED = 4x-x = 3x
S
AECB = 3*14 = 42
Ответ: площадь трапеции 42 см в кв.
Вы можете поблагодарить автора, написать свои претензии или предложения на
странице 'Про нас'
Другие задачи из этого раздела
Стороны AC, AB, BC треугольника ABC равны 2√5, √10 и 2 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если /KAC>90°.
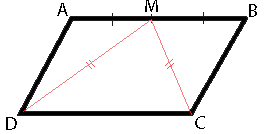 В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его медианой.
2) Диагонали прямоугольника равны.
3) У любой трапеции боковые стороны равны.
 В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
 На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

 Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB. Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма. 1) Отметим точку М на АB, так чтобы AM=MB
1) Отметим точку М на АB, так чтобы AM=MB В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника. На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Комментарии: