
 В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
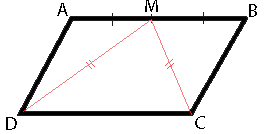
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники DAM и MBC. AM=MB, т.к. точка M - середина AB, MC=MD (из условия задачи), AD=BC (по свойству параллелограмма). Соответственно, треугольники DAM и MBC равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /DAM=/MBC.
AD||BC (по определению параллелограмма), рассмотрим сторону AB как секущую к этим параллельным сторонам. Тогда получается, что сумма углов DAM и MBC равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону AD как секущую к этим параллельным сторонам.
/DAM и /ADC - внутренние односторонние. Следовательно их сумма равна 180°. А так как /DAM=90°, то /ADC тоже равен 90°.
Аналогично доказывается, что /BCD тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
 Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
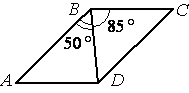 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
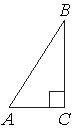 В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Комментарии: