
На координатной прямой отмечено число a.

Из следующих утверждений выберите верное.
1) (a-6)2>1
2) (a-5)2<1
3) a2<25
4) a2>36
По координатной прямой видно, что:
5<a<6
Вычтем 6 из каждого члена неравенства:
5-6<a-6<6-6
-1<a-6<0
И возведем каждый член неравенства в квадрат, так как в неравенстве все числа отрицательные, то при возведении в квадрат знак меняется на противополжный:
(-1)2>
(a-6)2>
02
1>(a-6)2>
0
Посмотрим на первую часть неравенства:
1>(a-6)2 - очевидно, что утверждение 1) неверно
Вернемся к первоначальному неравенству:
5<a<6
Вычтем 5 из каждого члена неравенства:
5-5<a-5<6-5
0<a-5<1
возведем в квадрат, все числа положительные, поэтому знак неравенства неменяется:
02>(a-5)2>12
0>(a-5)2>1
Посмотрим на вторую часть неравенства:
(a-5)2>1 - т.е. утверждение 2) верно
Вернемся к первоначальному неравенству:
5<a<6
Возведем в квадрат:
52<a2<62
25<a2<36
Из первой части неравенства видно, что утверждение 3) неверно, а из второй части неравенства видно, что и утверждение 4) неверно.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Решение какого из данных неравенств изображено на рисунке?

1) x2-x<0
2) x2-1<0
3) x2-1>0
4) x2-x>0
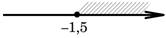
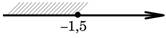
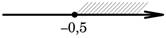
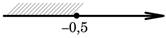
На каком рисунке изображено множество решений неравенства x-1≤3x+2?
1) 
2) 
3) 
4) 
Какому из следующих чисел соответствует точка, отмеченная на координатной прямой?

1) 3/11
2) 7/11
3) 8/11
4) 13/11
Постройте график функции 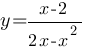 и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
На каком рисунке изображено множество решений системы неравенств
 x>-1,
x>-1,
3-x>0?
1) 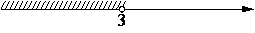
2) 
3) система не имеет решений
4) 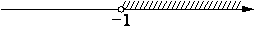
Комментарии: