Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=11 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Рассмотрим треугольники ADC и CBD.
∠DCA=∠CBA (т.к. ∠DCA равен половине градусной меры дуги CA по четвертому свойству углов, связанных с окружностью, и на эту же дугу опирается
вписанный угол CBA, который тоже равен половине градусной меры дуги, на которую опирается по
теореме).
∠CDB - общий для обоих треугольников, следовательно, по
признаку подобия, треугольники ADC и CBD -
подобны.
Следовательно, по определению подобных треугольников запишем:
CD/BD=AC/BC=AD/CD
AC/BC=AM/MB=11/16 (по первому
свойству биссектрисы).
Из этих равенств выписываем:
AD=CD*11/16
BD=CD*16/11, (BD=AD+AB=AD+16+11=AD+27)
AD+27=CD*16/11
CD*11/16+27=CD*16/11
27=CD*16/11-CD*11/16
27=(16*16*CD-11*11*CD)/176
27*176=CD(256-121)
CD=4752/135=35,2
Ответ: CD=35,2
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
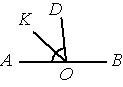Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: